逻辑回归二分类

广义线性回归到逻辑回归

什么是逻辑回归

逻辑回归不是一个回归算法，而是一个分类算法。逻辑回归基于多元线性回归算法，因此是一个线性分类器。逻辑回归中有一条非常重要的S型曲线，对应的函数是Sigmoid函数：

$f(x) = \frac{1}{1 + e^{-x}}$

这个函数有一个很好的特性，其导数可以用自身表示：

$f'(x) = \frac{e^{-x}}{(1 + e^{-x})^2} = f(x) \cdot (1 - f(x))$

以下是Sigmoid函数的Python实现和绘制代码：

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.linspace(-5, 5, 100)
y = sigmoid(x)
plt.plot(x, y, color='green')
plt.show()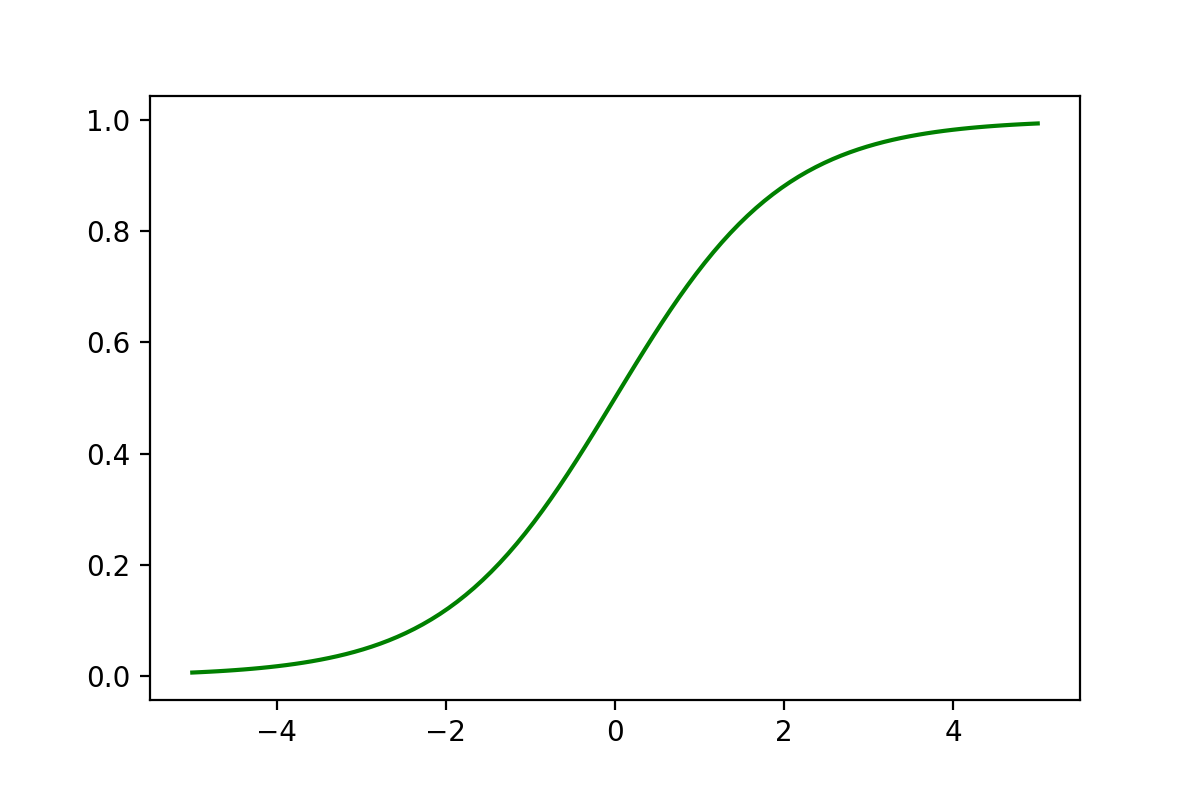

Sigmoid函数介绍

逻辑回归在多元线性回归的基础上将结果缩放到0~1之间。$h_{\theta}(x)$越接近1，越可能是正例；越接近0，越可能是负例。以0.5为分类边界，将数据分为两类：

$h_{\theta}(x) = g(\theta^T x) = \frac{1}{1 + e^{-\theta^T x}}$

当$h_{\theta}(x) = 0.5$时，即$\theta^T x = 0$，找到$\theta$的解。

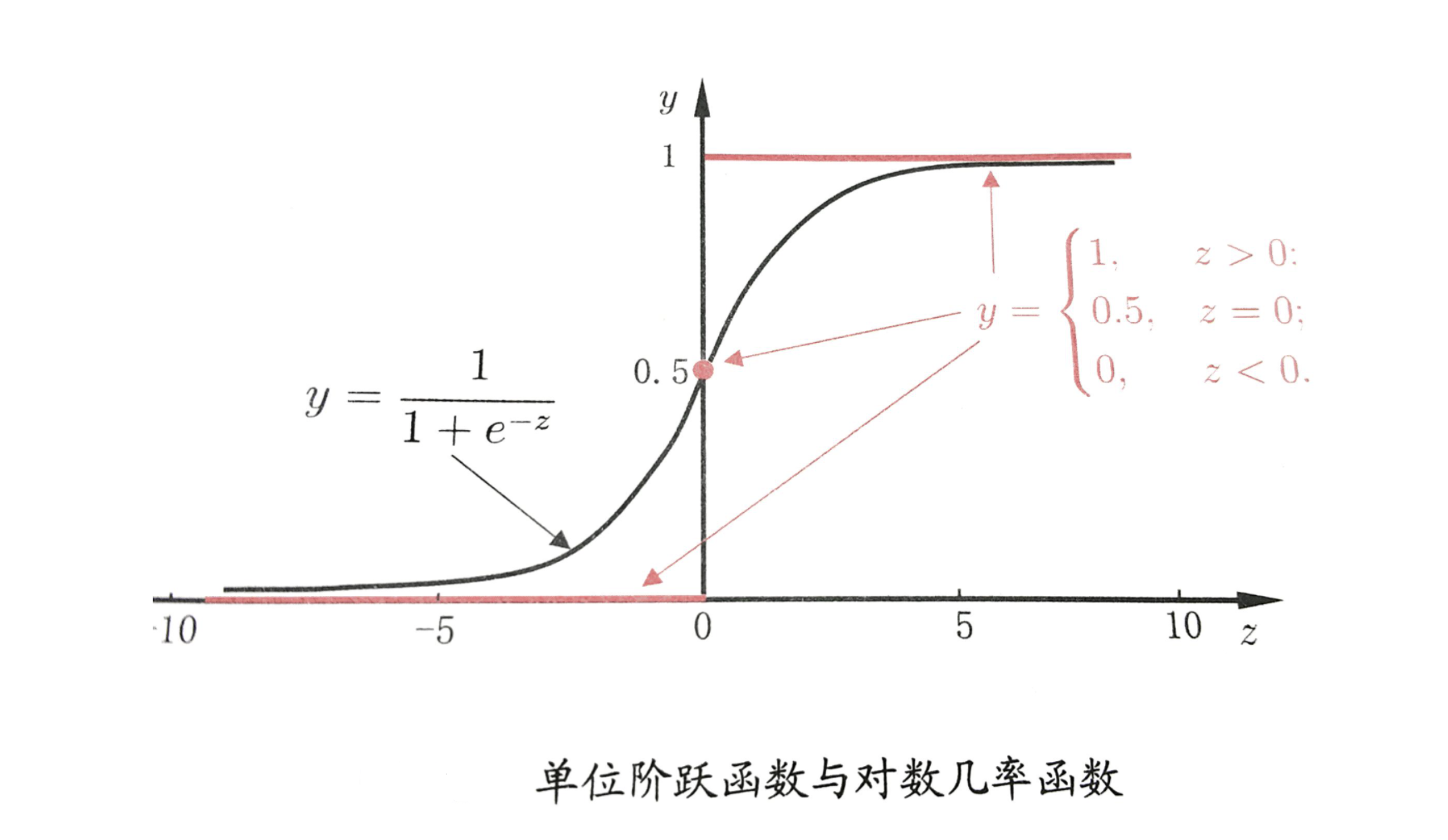
求解过程如下：

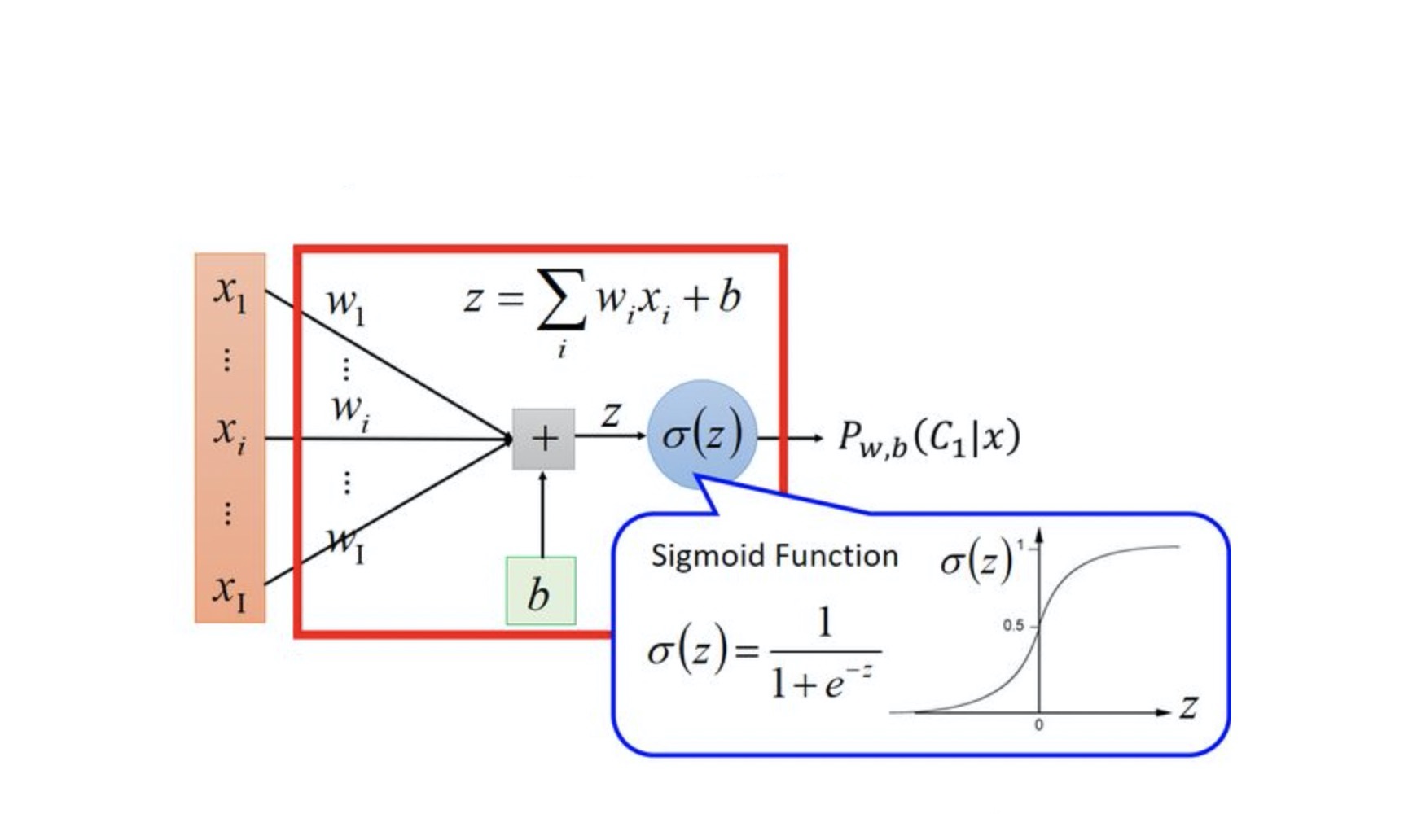
二分类的概率分布

二分类问题中，正例和负例的概率之和为1。伯努利分布描述了只有两种可能结果的试验，其概率函数为：

$f(x | p) = \begin{cases} p^x (1 - p)^{1 - x}, & x = 1, 0 \\ 0, & x \neq 1, 0 \end{cases}$

逻辑回归将正例标签设为1，负例标签设为0。

逻辑回归公式推导

损失函数推导

逻辑回归使用最大似然估计思想，找到使训练集概率最大的$\theta$：

$P(y | x; \theta) = \begin{cases} h_{\theta}(x), & y = 1 \\ 1 - h_{\theta}(x), & y = 0 \end{cases}$

整合为：

$P(y | x; \theta) = (h_{\theta}(x))^y (1 - h_{\theta}(x))^{1 - y}$

似然函数为：

$L(\theta) = \prod_{i=1}^n (h_{\theta}(x^{(i)}))^{y^{(i)}} (1 - h_{\theta}(x^{(i)}))^{1 - y^{(i)}}$

取自然对数得到对数似然函数：

$l(\theta) = \sum_{i=1}^n \left[ y^{(i)} \ln(h_{\theta}(x^{(i)})) + (1 - y^{(i)}) \ln(1 - h_{\theta}(x^{(i)})) \right]$

损失函数为：

$J(\theta) = -l(\theta) = -\sum_{i=1}^n \left[ y^{(i)} \ln(h_{\theta}(x^{(i)})) + (1 - y^{(i)}) \ln(1 - h_{\theta}(x^{(i)})) \right]$

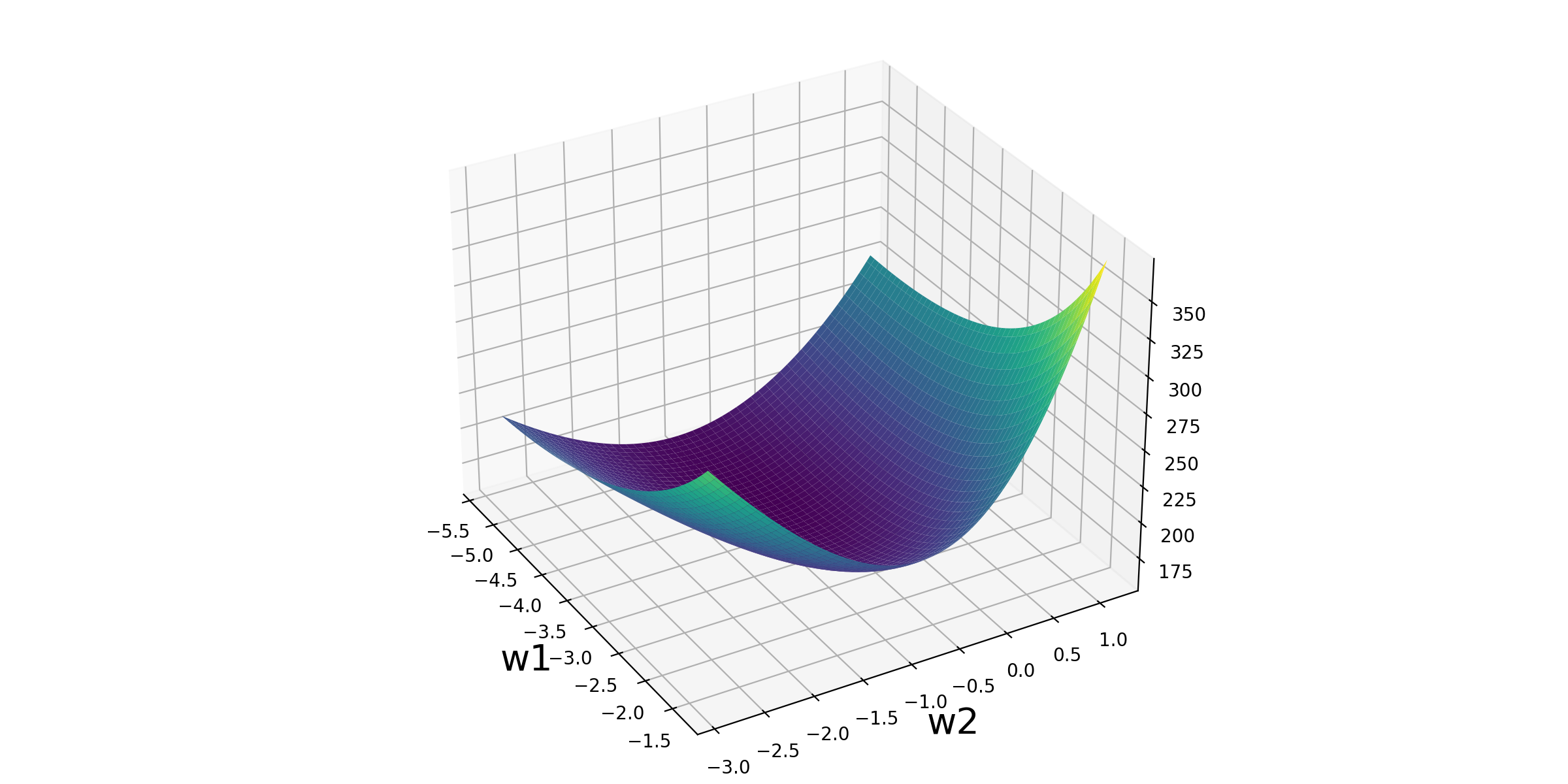
立体化呈现

以下是逻辑回归损失函数可视化的Python代码：

from sklearn import datasets
from sklearn.linear_model import LogisticRegression
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.preprocessing import scale

# 加载乳腺癌数据
data = datasets.load_breast_cancer()
X, y = scale(data['data'][:, :2]), data['target']

# 求出最优解
lr = LogisticRegression()
lr.fit(X, y)

# 提取参数
w1 = lr.coef_[0, 0]
w2 = lr.coef_[0, 1]

# 定义Sigmoid函数和损失函数
def sigmoid(X, w1, w2):
    z = w1 * X[0] + w2 * X[1]
    return 1 / (1 + np.exp(-z))

def loss_function(X, y, w1, w2):
    loss = 0
    for x_i, y_i in zip(X, y):
        p = sigmoid(x_i, w1, w2)
        loss += -y_i * np.log(p) - (1 - y_i) * np.log(1 - p)
    return loss

# 参数取值空间
w1_space = np.linspace(w1 - 2, w1 + 2, 100)
w2_space = np.linspace(w2 - 2, w2 + 2, 100)
loss1_ = np.array([loss_function(X, y, i, w2) for i in w1_space])
loss2_ = np.array([loss_function(X, y, w1, i) for i in w2_space])

# 数据可视化
fig1 = plt.figure(figsize=(12, 9))
plt.subplot(2, 2, 1)
plt.plot(w1_space, loss1_)
plt.subplot(2, 2, 2)
plt.plot(w2_space, loss2_)
w1_grid, w2_grid = np.meshgrid(w1_space, w2_space)
loss_grid = loss_function(X, y, w1_grid, w2_grid)
plt.subplot(2, 2, 3)
plt.contour(w1_grid, w2_grid, loss_grid, 20)
plt.subplot(2, 2, 4)
plt.contourf(w1_grid, w2_grid, loss_grid, 20)
plt.savefig('/post/LogisticRegression/4-损失函数可视化.png', dpi=200)

# 3D可视化
fig2 = plt.figure(figsize=(12, 6))
ax = Axes3D(fig2)
ax.plot_surface(w1_grid, w2_grid, loss_grid, cmap='viridis')
plt.xlabel('w1', fontsize=20)
plt.ylabel('w2', fontsize=20)
ax.view_init(30, -30)
plt.savefig('/post/LogisticRegression/5-损失函数可视化.png', dpi=200)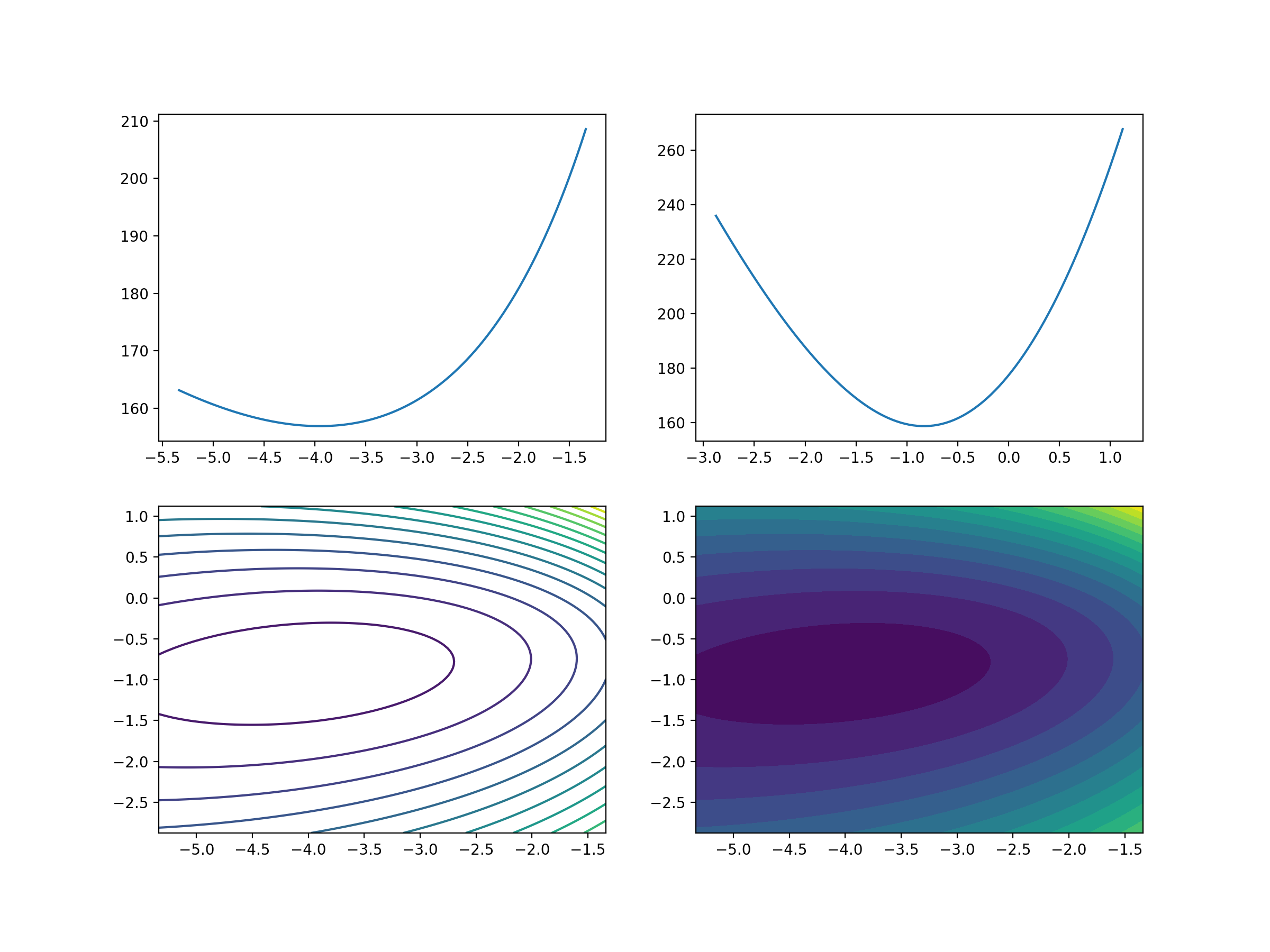

逻辑回归迭代公式

函数特性

逻辑回归参数更新规则与线性回归类似：

$\theta_j^{t + 1} = \theta_j^t - \alpha \frac{\partial}{\partial \theta_j} J(\theta)$

其中，$\alpha$是学习率。

逻辑回归函数及其导数特性：

$h_{\theta}(x) = g(\theta^T x) = \frac{1}{1 + e^{-z}}$

$g'(z) = g(z) \cdot (1 - g(z))$

求导过程

逻辑回归损失函数求导：

$\frac{\partial}{\partial \theta_j} J(\theta) = \sum_{i=1}^n (h_{\theta}(x^{(i)}) - y^{(i)}) x_j^{(i)}$

参数迭代更新公式：

$\theta_j^{t+1} = \theta_j^t - \alpha \sum_{i=1}^n (h_{\theta}(x^{(i)}) - y^{(i)}) x_j^{(i)}$

代码实战

以下是逻辑回归在鸢尾花数据集上的代码实现：

import numpy as np
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split

# 数据加载
iris = datasets.load_iris()

# 数据提取与筛选
X = iris['data']
y = iris['target']
cond = y != 2
X = X[cond]
y = y[cond]

# 数据拆分
X_train, X_test, y_train, y_test = train_test_split(X, y)

# 模型训练
lr = LogisticRegression()
lr.fit(X_train, y_train)

# 模型预测
y_predict = lr.predict(X_test)
print('测试数据真实类别是：', y_test)
print('测试数据预测类别是：', y_predict)
print('测试数据预测概率是：\n', lr.predict_proba(X_test))

# 线性方程和Sigmoid函数
b = lr.intercept_
w = lr.coef_

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

z = X_test.dot(w.T) + b
p_1 = sigmoid(z)
p_0 = 1 - p_1
p = np.concatenate([p_0, p_1], axis=1)
print(p)

逻辑回归做多分类

One-Vs-Rest思想

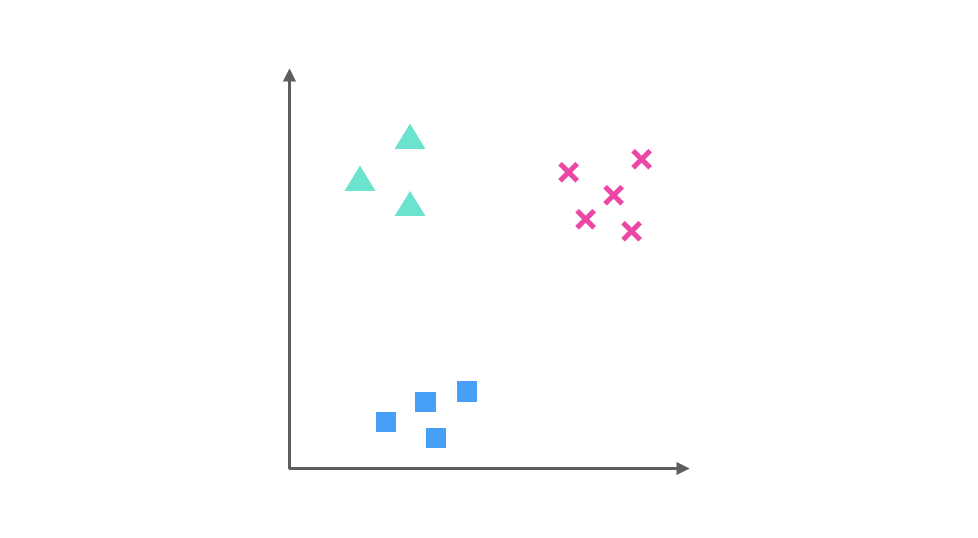
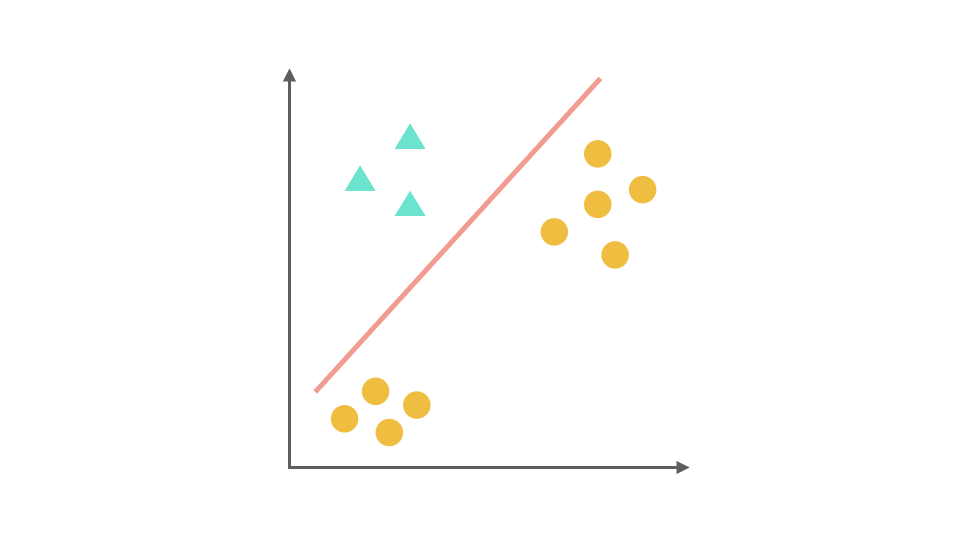
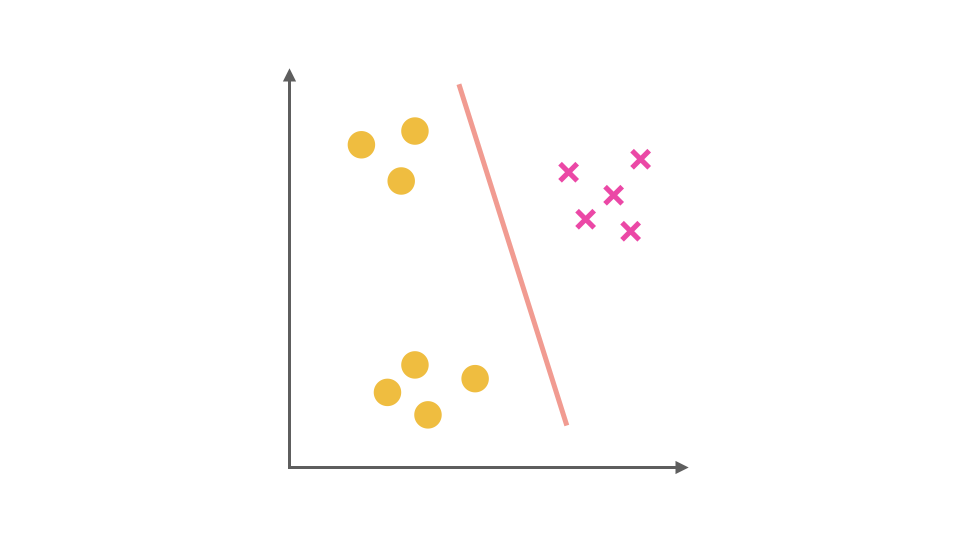
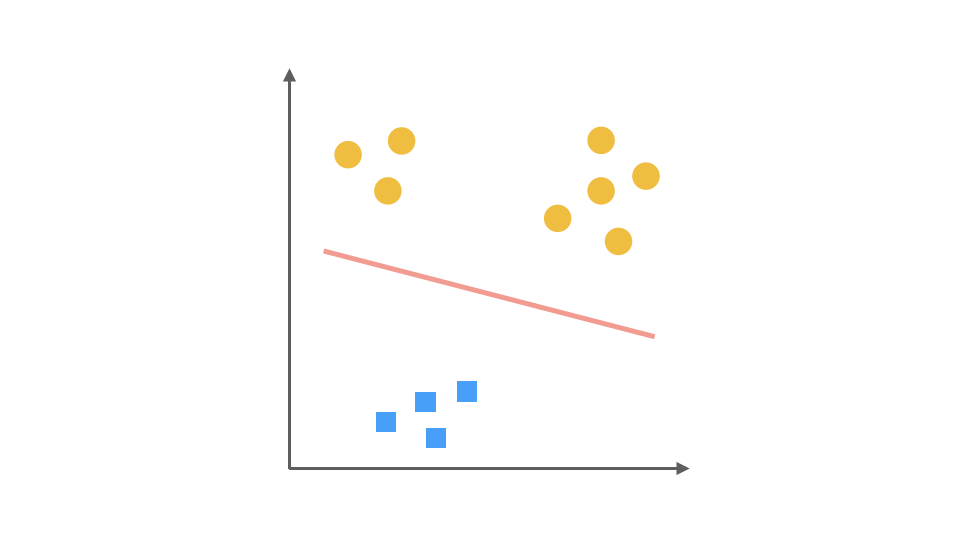
对于多分类问题，逻辑回归可以通过One-Vs-Rest（OvR）策略将其转化为多个二分类问题。以三分类问题为例：

1. 将第一个类别作为正类，其余作为负类，训练第一个分类器。
2. 将第二个类别作为正类，其余作为负类，训练第二个分类器。
3. 将第三个类别作为正类，其余作为负类，训练第三个分类器。

预测时，计算每个分类器的概率，选择概率最高的类别作为预测结果。

代码实战

以下是逻辑回归在鸢尾花三分类问题上的代码实现：

import numpy as np
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split

# 数据加载
iris = datasets.load_iris()

# 数据提取
X = iris['data']
y = iris['target']

# 数据拆分
X_train, X_test, y_train, y_test = train_test_split(X, y)

# 模型训练，使用One-Vs-Rest策略
lr = LogisticRegression(multi_class='ovr')
lr.fit(X_train, y_train)

# 模型预测
y_predict = lr.predict(X_test)
print('测试数据真实类别是：', y_test)
print('测试数据预测类别是：', y_predict)
print('测试数据预测概率是：\n', lr.predict_proba(X_test))

# 线性方程和Sigmoid函数
b = lr.intercept_
w = lr.coef_

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

z = X_test.dot(w.T) + b
p = sigmoid(z)
p = p / p.sum(axis=1).reshape(-1, 1)
print(p)

多分类Softmax回归

多项分布指数分布族形式

Softmax回归假设数据服从多项分布。对于有k个类别的分类问题，每个类别的概率为：

$p(y = i | x; \theta) = \frac{e^{\theta_i^T x}}{\sum_{j=1}^k e^{\theta_j^T x}}$

广义线性模型推导Softmax回归

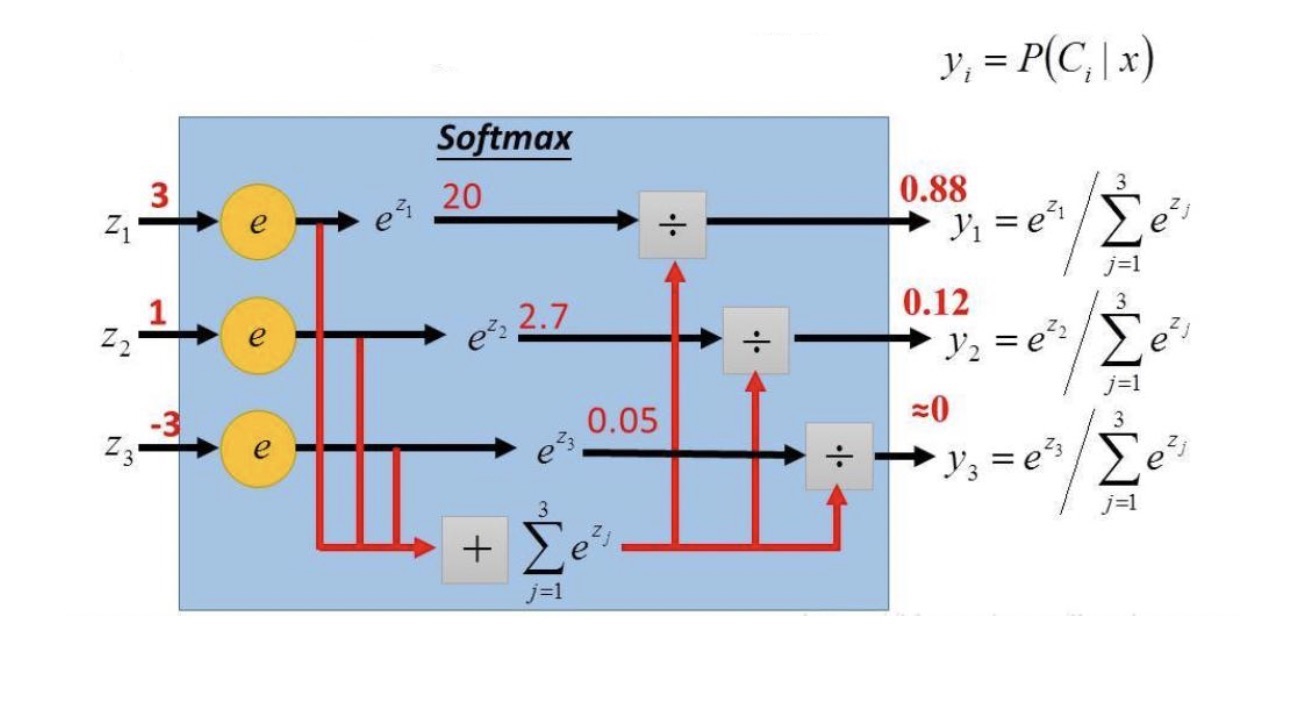
Softmax函数将多个线性方程的输出转换为概率分布：

$h_{\theta}(x) = \begin{cases} \frac{e^{\theta_1^T x}}{\sum_{j=1}^k e^{\theta_j^T x}}, & y = 1 \\ \frac{e^{\theta_2^T x}}{\sum_{j=1}^k e^{\theta_j^T x}}, & y = 2 \\ \vdots \\ \frac{e^{\theta_k^T x}}{\sum_{j=1}^k e^{\theta_j^T x}}, & y = k \end{cases}$

代码实战

以下是Softmax回归在鸢尾花三分类问题上的代码实现：

import numpy as np
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split

# 数据加载
iris = datasets.load_iris()

# 数据提取
X = iris['data']
y = iris['target']

# 数据拆分
X_train, X_test, y_train, y_test = train_test_split(X, y)

# 模型训练，使用Softmax回归
lr = LogisticRegression(multi_class='multinomial', max_iter=5000)
lr.fit(X_train, y_train)

# 模型预测
y_predict = lr.predict(X_test)
print('测试数据真实类别是：', y_test)
print('测试数据预测类别是：', y_predict)
print('测试数据预测概率是：\n', lr.predict_proba(X_test))

# 线性方程和Softmax函数
b = lr.intercept_
w = lr.coef_

def softmax(z):
    return np.exp(z) / np.exp(z).sum(axis=1).reshape(-1, 1)

z = X_test.dot(w.T) + b
p = softmax(z)
print(p)

逻辑回归与Softmax回归对比

逻辑回归是Softmax回归的特例

当k=2时，Softmax回归退化为逻辑回归：

$h_{\theta}(x) = \frac{1}{1 + e^{\theta^T x}}$

Softmax损失函数

Softmax回归的损失函数是交叉熵损失：

$J(\theta) = -\sum_{i=1}^n \sum_{j=1}^k I\{y^{(i)} = j\} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{\theta_l^T x^{(i)}}}$